Below it is proved that the internal energy of an ideal gas depends only on its temperature. Therefore,
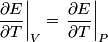 and therefore 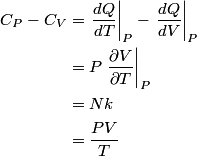 The process is adiabatic, so from the first law of thermodynamics 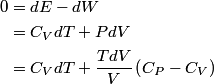 which implies that 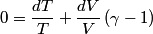 Using integration by parts then gives that 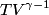 is constant. Therefore, answer (C) is correct. is constant. Therefore, answer (C) is correct.Proof that the internal energy of an ideal gas depends only on its temperature: 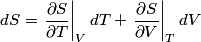 implies that 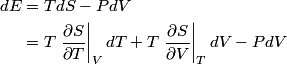 implies that  From 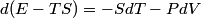 and the equality of mixed partial derivatives it follows that 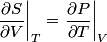 Therefore, equation 1 becomes 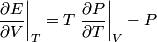 which equals 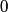 for an ideal gas. This completes the proof. for an ideal gas. This completes the proof. |